Worksheet
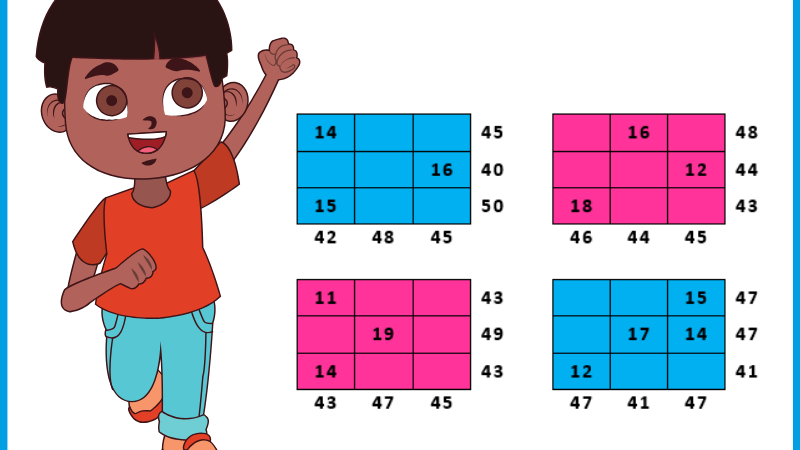
Addition puzzle boxes
More or less
Array hooray!
Number pattern investigation
Roll and Fill
Roll and Fill Resources needed paper, pencils, dices Instructions to play 1.Print or draw a whole part grid sheet 2.Handout grid and two dices to learners in pairs 3. Learners must roll both dices 4.Write the two rolled numbers in the bottom of the whole -part diagram 5.Add ... » Learn More about Roll and Fill